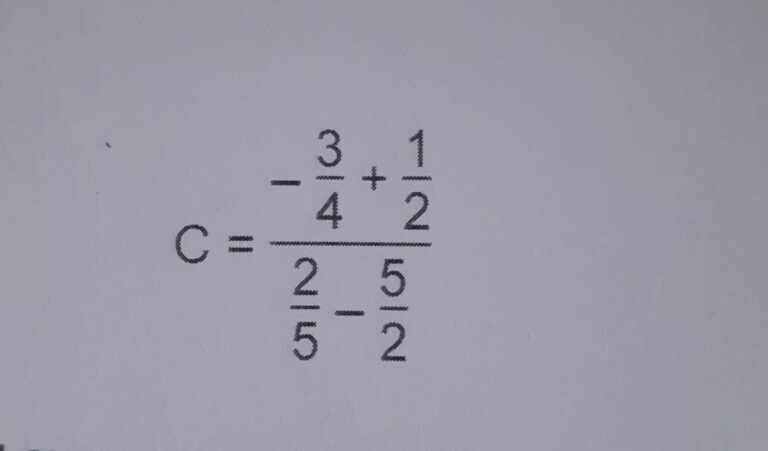Calcul des fractions
Introduction
Les fractions sont des nombres qui représentent une partie d\’un tout. Elles sont composées d\’un numérateur (le nombre au-dessus de la barre) et d\’un dénominateur (le nombre en dessous de la barre). Les fractions sont utilisées dans de nombreux domaines, tels que les mathématiques, la physique, la chimie et l\’ingénierie.
Calcul plus détaillé
Pour additionner ou soustraire des fractions, les dénominateurs doivent être les mêmes. Pour cela, il faut trouver le plus petit multiple commun des dénominateurs et convertir les fractions en fractions équivalentes avec ce dénominateur commun. Ensuite, on peut simplement ajouter ou soustraire les numérateurs.
Pour multiplier des fractions, il suffit de multiplier les numérateurs entre eux et les dénominateurs entre eux. Pour diviser des fractions, on multiplie la première fraction par l\’inverse de la deuxième fraction.
Signification et applications
Les fractions sont utilisées pour représenter des parts d\’un tout, comme des portions d\’une pizza ou des quantités de liquide dans une recette. En mathématiques, les fractions sont essentielles pour résoudre des problèmes impliquant des quantités partielles. En physique et en chimie, les fractions sont utilisées pour calculer des ratios et des proportions. En ingénierie, les fractions sont utilisées pour mesurer des distances, des angles et des quantités.
Concept de Variation en Pourcentage
La variation en pourcentage est un concept important en mathématiques qui permet de mesurer les changements relatifs dans une quantité par rapport à une valeur de référence. Elle est souvent utilisée pour comparer des données dans divers domaines tels que l\’économie, les finances, les sciences et le commerce.
Applications
- Finance : En finance, la variation en pourcentage est utilisée pour analyser les rendements des investissements. Par exemple, si le prix d\’une action a augmenté de 10 %, cela signifie qu\’il a augmenté de 10 % par rapport à son prix initial.
- Commerce : Dans le commerce, la variation en pourcentage est utilisée pour calculer les remises, les promotions et les hausses de prix. Par exemple, si un produit est en promotion avec une réduction de 20 %, cela signifie que le prix du produit a diminué de 20 % par rapport à son prix initial.
- Sciences : En sciences, la variation en pourcentage est utilisée pour analyser les changements dans les données expérimentales. Par exemple, si la température a augmenté de 5 %, cela signifie qu\’elle a augmenté de 5 % par rapport à sa valeur initiale.
Éléments interactifs
Pour améliorer la compréhension et l\’engagement avec les variations en pourcentage, voici quelques suggestions d\’éléments interactifs :
- Exercices interactifs : Proposez des exercices pratiques où les apprenants peuvent calculer des variations en pourcentage dans différents contextes.
- Études de cas du monde réel : Présentez des exemples concrets de variations en pourcentage dans des situations réelles pour montrer aux apprenants comment ce concept est appliqué dans la pratique.
- Outils de visualisation : Utilisez des graphiques, des diagrammes et d\’autres outils visuels pour illustrer les variations en pourcentage et rendre le concept plus concret et facile à comprendre.
En intégrant ces éléments interactifs dans l\’apprentissage des variations en pourcentage, les apprenants pourront renforcer leur compréhension et leur maîtrise de ce concept essentiel en mathématiques.
| Méthode de mesure | Principe de mesure | Précision | Facilité d\’utilisation | Coût | Applications typiques | Exemples |
|---|---|---|---|---|---|---|
| Méthode 1 | Principe de mesure de la méthode 1 | Haute | Facile | Élevé | Application 1, Application 2 | Exemple 1, Exemple 2 |
| Méthode 2 | Principe de mesure de la méthode 2 | Moyenne | Moyenne | Moyen | Application 3, Application 4 | Exemple 3, Exemple 4 |
| Méthode 3 | Principe de mesure de la méthode 3 | Basse | Difficile | Bas | Application 5, Application 6 | Exemple 5, Exemple 6 |