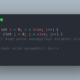
La médiane
La médiane est une mesure de tendance centrale qui représente la valeur centrale d\’un ensemble de données ordonnées. Elle divise l\’ensemble en deux parties égales, avec autant de valeurs au-dessus et en dessous d\’elle.
Calcul de la médiane :
Pour calculer la médiane, vous devez d\’abord ordonner les données de manière croissante ou décroissante. Ensuite, si le nombre d\’observations est impair, la médiane est la valeur au milieu de la série. Si le nombre d\’observations est pair, la médiane est la moyenne des deux valeurs du milieu.
Formule pour la médiane :
- Si n est impair : Médiane = Valeur[n/2]
- Si n est pair : Médiane = (Valeur[n/2] + Valeur[(n/2) + 1]) / 2
Signification et applications de la médiane :
La médiane est souvent utilisée pour représenter une valeur typique dans un ensemble de données, en particulier lorsqu\’il y a des valeurs extrêmes qui pourraient fausser la moyenne. Elle est couramment utilisée en statistiques, en économie, en sciences sociales et dans d\’autres domaines où la représentation d\’une valeur centrale est importante.
Par exemple, en économie, la médiane des revenus d\’une population peut donner une meilleure indication de la situation financière moyenne des individus que la moyenne arithmétique, qui peut être biaisée par les revenus extrêmement élevés ou bas.
Concept de variation en pourcentage
La variation en pourcentage est un concept important dans de nombreux domaines, car elle permet de mesurer le changement relatif d\’une valeur par rapport à une valeur de référence. Elle est souvent utilisée pour comparer des données sur une période donnée ou entre différentes entités.
Applications
La variation en pourcentage est largement utilisée dans les domaines de la finance, du commerce, de l\’économie, des sciences et même dans la vie quotidienne. Voici quelques exemples d\’applications courantes :
- En finance, la variation en pourcentage est utilisée pour analyser les performances des investissements, les fluctuations des taux de change et les variations des prix des actifs.
- En commerce, elle est utilisée pour évaluer les ventes, les marges bénéficiaires et les promotions marketing.
- En économie, elle est utilisée pour étudier l\’inflation, le chômage et la croissance économique.
- Dans les sciences, elle est utilisée pour analyser les données expérimentales et les tendances de croissance.
Éléments interactifs
Pour améliorer la compréhension et l\’engagement avec la variation en pourcentage, voici quelques suggestions d\’éléments interactifs :
- Exercices interactifs : Créez des exercices qui permettent aux apprenants de calculer la variation en pourcentage et de l\’appliquer à des situations réelles.
- Études de cas du monde réel : Proposez des études de cas qui mettent en lumière l\’importance de la variation en pourcentage dans divers domaines et industries.
- Outils de visualisation : Utilisez des graphiques et des tableaux interactifs pour illustrer visuellement la variation en pourcentage et faciliter sa compréhension.
En combinant ces éléments interactifs avec des explications claires et des exemples concrets, les apprenants seront en mesure de maîtriser le concept de variation en pourcentage et de l\’appliquer efficacement dans leur domaine d\’étude ou de travail.
| Méthode de mesure | Principe de mesure | Précision | Facilité d\’utilisation | Coût | Applications typiques | Exemples |
|---|---|---|---|---|---|---|
| Méthode A | Mesure directe du [mot-clé] à l\’aide d\’un appareil spécifique | Très précise | Requiert une formation spécifique | Élevé | Recherche en laboratoire, contrôle qualité | Spectrophotomètre UV-Vis pour mesurer la concentration de [mot-clé] |
| Méthode B | Analyse indirecte du [mot-clé] à partir d\’autres paramètres mesurables | Variable en fonction des paramètres utilisés | Relativement facile à mettre en œuvre | Modéré | Surveillance environnementale, analyse clinique | Méthode colorimétrique pour estimer la concentration de [mot-clé] |
| Méthode C | Évaluation qualitative du [mot-clé] basée sur des observations visuelles ou sensorielles | Moins précise que les méthodes quantitatives | Facile à mettre en œuvre sans équipement spécialisé | Faible | Détection rapide sur le terrain, contrôle de la qualité des aliments | Test de détection visuelle pour la présence de [mot-clé] |