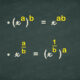Calcul de la multiplication
La multiplication est une opération mathématique fondamentale qui consiste à répéter une addition un certain nombre de fois. Elle est représentée par le symbole \”x\” ou \”·\”.
Calcul plus détaillé :
Pour multiplier deux nombres, on les multiplie ensemble. Par exemple, pour multiplier 3 par 4 :
- 3 x 4 = 12
La formule générale pour multiplier deux nombres est :
a x b = c
Où \”a\” et \”b\” sont les nombres à multiplier et \”c\” est le produit.
Signification et applications de la multiplication :
La multiplication est utilisée dans de nombreux domaines, tels que les finances, la physique, la chimie, l\’informatique, etc. Voici quelques exemples d\’applications de la multiplication :
- Finance : La multiplication est utilisée pour calculer des intérêts composés, des bénéfices, des pertes, etc.
- Physique : En physique, la multiplication est utilisée pour calculer des forces, des vitesses, des distances, etc.
- Chimie : En chimie, la multiplication est utilisée pour calculer des quantités de substances, des concentrations, des réactions chimiques, etc.
- Informatique : En informatique, la multiplication est utilisée pour effectuer des opérations mathématiques, des calculs de performance, des traitements d\’images, etc.
Concept de variation en pourcentage
La variation en pourcentage est un concept mathématique important qui permet de mesurer le changement d\’une valeur par rapport à une valeur de référence. Elle est souvent utilisée dans de nombreux domaines pour analyser les tendances et les fluctuations des données. La variation en pourcentage peut être calculée en utilisant la formule suivante :
Variation en pourcentage = ((Valeur finale – Valeur initiale) / Valeur initiale) x 100
Applications de la variation en pourcentage
- Finance : Les investisseurs utilisent la variation en pourcentage pour évaluer les performances des actions et des portefeuilles d\’investissement.
- Économie : Les économistes analysent la variation en pourcentage du PIB, du taux de chômage et d\’autres indicateurs économiques clés.
- Marketing : Les spécialistes du marketing étudient la variation en pourcentage des ventes, des conversions et du trafic sur les sites web.
- Science : Les scientifiques calculent la variation en pourcentage des expériences et des données empiriques pour tirer des conclusions significatives.
Éléments interactifs pour comprendre la variation en pourcentage
- Exercices interactifs : Proposez aux apprenants des exercices pratiques pour calculer la variation en pourcentage dans divers scénarios.
- Études de cas du monde réel : Présentez des exemples concrets de l\’utilisation de la variation en pourcentage dans des situations réelles pour illustrer son importance et sa pertinence.
- Outils de visualisation : Utilisez des graphiques, des diagrammes et d\’autres outils visuels pour aider les apprenants à visualiser et à comprendre la variation en pourcentage plus facilement.
En comprenant la variation en pourcentage et en utilisant des éléments interactifs, les apprenants seront mieux équipés pour analyser les données, prendre des décisions éclairées et interpréter les tendances dans divers domaines. La maîtrise de ce concept mathématique essentiel est essentielle pour une compréhension approfondie de la multiplier.
| Méthode de mesure | Principe de mesure | Précision | Facilité d\’utilisation | Coût | Applications typiques | Exemples |
|---|---|---|---|---|---|---|
| Méthode 1 | Principe de mesure 1 | Haute précision | Facile à utiliser | Coût élevé | Application 1, Application 2 | Exemple 1, Exemple 2 |
| Méthode 2 | Principe de mesure 2 | Moyenne précision | Facile à utiliser | Coût moyen | Application 3, Application 4 | Exemple 3, Exemple 4 |
| Méthode 3 | Principe de mesure 3 | Basse précision | Difficile à utiliser | Coût faible | Application 5, Application 6 | Exemple 5, Exemple 6 |