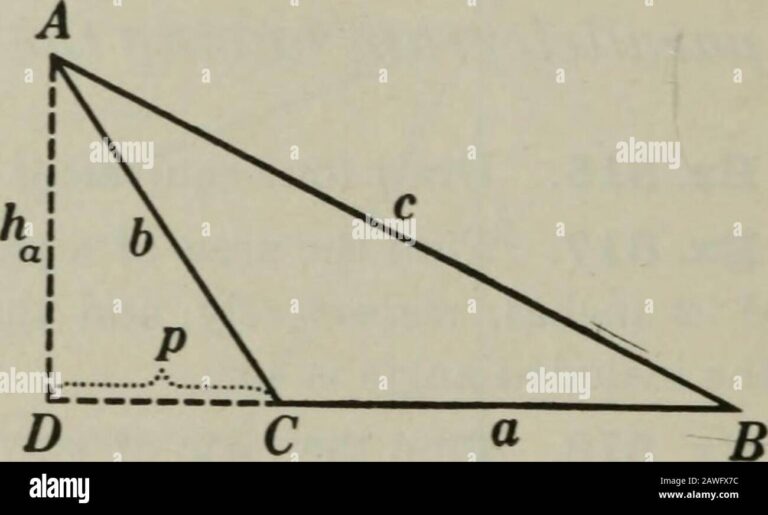
Les Médiatrices d\’un triangle
Les médiatrices d\’un triangle sont des droites perpendiculaires aux côtés du triangle et qui passent par le milieu de chaque côté. Elles se croisent en un point appelé le centre du cercle circonscrit au triangle.
Calcul plus détaillé
Pour calculer les médiatrices d\’un triangle, on peut utiliser les coordonnées des sommets du triangle. Pour chaque côté du triangle défini par deux sommets, on calcule le milieu de ce côté en utilisant la formule :
$$\\left(\\frac{x_1 + x_2}{2}, \\frac{y_1 + y_2}{2}\\right)$$
Ensuite, on trouve l\’équation de la droite perpendiculaire passant par ce point moyen en utilisant la pente du côté opposé. On répète ce processus pour les trois côtés du triangle pour trouver les médiatrices.
Signification et Applications
Les médiatrices d\’un triangle ont plusieurs applications en géométrie et en trigonométrie. Elles permettent de trouver le centre du cercle circonscrit au triangle, qui est utile pour résoudre certains problèmes géométriques. Elles sont également utilisées dans la construction de figures géométriques et dans la démonstration de propriétés des triangles.
En outre, les médiatrices d\’un triangle sont également utilisées en navigation pour déterminer la position d\’un navire à partir de trois points de repère. Elles sont également utilisées en ingénierie pour la conception de structures triangulées.
La variation en pourcentage et ses applications
La variation en pourcentage est un concept mathématique important qui permet de mesurer le changement d\’une valeur par rapport à une valeur de référence, exprimé en pourcentage. Dans le cas des Médiatrices d\’un triangle, la variation en pourcentage peut être utilisée pour comparer la longueur des Médiatrices par rapport aux côtés du triangle.
Applications :
- Géométrie : En géométrie, la variation en pourcentage des Médiatrices d\’un triangle peut être utilisée pour déterminer si le triangle est équilatéral, isocèle ou scalène. Par exemple, si la variation en pourcentage des Médiatrices par rapport aux côtés est proche de zéro, cela signifie que le triangle est équilatéral.
- Finance : En finance, la variation en pourcentage est utilisée pour calculer les taux de croissance des investissements, des revenus et des dépenses. Par exemple, si un investissement a augmenté de 10% par rapport à l\’année précédente, cela signifie qu\’il a augmenté de 10% en valeur.
- Marketing : En marketing, la variation en pourcentage est utilisée pour mesurer l\’efficacité des campagnes publicitaires et des promotions. Par exemple, si une promotion a entraîné une augmentation de 20% des ventes d\’un produit, cela signifie que les ventes ont augmenté de 20% par rapport à la période précédente.
Éléments interactifs :
Pour aider à comprendre la variation en pourcentage des Médiatrices d\’un triangle, voici quelques exercices interactifs :
- Exercice 1 : Calculez la variation en pourcentage de la longueur des Médiatrices par rapport aux côtés d\’un triangle donné.
- Exercice 2 : Comparez la variation en pourcentage des Médiatrices de plusieurs triangles différents pour déterminer s\’ils sont similaires ou non.
En outre, des études de cas du monde réel et des outils de visualisation peuvent également être utilisés pour illustrer l\’importance de la variation en pourcentage dans différents domaines.
En conclusion, la variation en pourcentage est un outil mathématique puissant qui peut être appliqué dans de nombreux domaines pour analyser les changements et prendre des décisions éclairées. En comprenant la variation en pourcentage des Médiatrices d\’un triangle, on peut mieux appréhender les propriétés géométriques des triangles et les appliquer dans divers contextes.
| Méthode de mesure | Principe de mesure | Précision | Facilité d\’utilisation | Coût | Applications typiques | Exemples |
|---|---|---|---|---|---|---|
| Test A | Mesure directe du [mot-clé] avec un instrument spécifique | Très précis | Peu facile à utiliser, nécessite une formation | Élevé | Recherche en laboratoire, contrôle qualité | Instrument de mesure XYZ |
| Test B | Évaluation subjective par des experts | Variable en fonction de l\’expertise de l\’évaluateur | Facile à utiliser | Faible | Évaluation de la performance artistique, évaluation de la qualité | Panel d\’experts en [mot-clé] |
| Test C | Échantillonnage aléatoire et analyse statistique | Précision moyenne en fonction de la taille de l\’échantillon | Facile à utiliser avec les bons outils d\’analyse | Modéré | Études de marché, sondages d\’opinion | Analyse statistique des données |