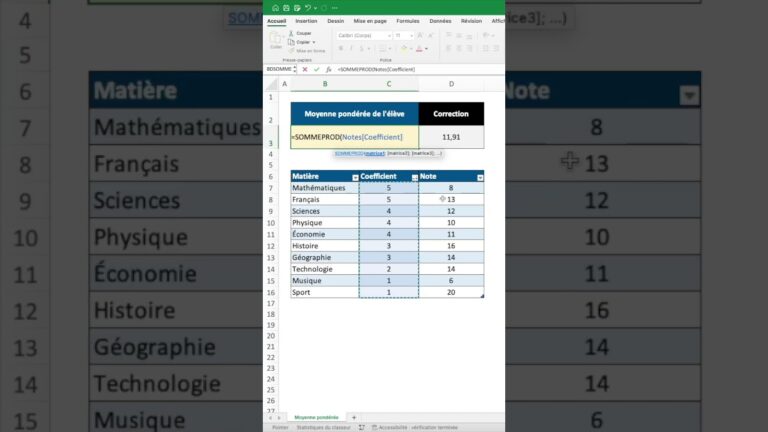
La Moyenne pondérée
La moyenne pondérée est une méthode de calcul de la moyenne d\’un ensemble de valeurs en tenant compte du poids de chaque valeur. Cela signifie que certaines valeurs peuvent avoir plus d\’influence sur le résultat final en fonction de leur poids.
Le concept de moyenne pondérée est un outil mathématique puissant qui permet de donner une importance différente à chaque élément d’un ensemble de données lors du calcul d’une moyenne. Dans cet article, nous allons explorer en détail ce concept et expliquer comment utiliser une calculatrice pour effectuer ces calculs. Nous discuterons également de la pertinence de ce concept dans divers contextes et fournirons de nombreux exemples concrets pour illustrer son utilisation. Nous analyserons les différences de poids dans le calcul de la moyenne et donnerons des conseils clairs aux lecteurs sur la façon de choisir des poids appropriés en fonction de la situation donnée.
Qu’est-ce que la moyenne pondérée ?
La moyenne pondérée est une méthode de calcul de la moyenne qui attribue un poids différent à chaque élément d’un ensemble de données. Contrairement à la moyenne arithmétique où tous les éléments sont considérés comme ayant la même importance, la moyenne pondérée permet de donner plus d’importance à certains éléments par rapport à d’autres.
Pour calculer la moyenne pondérée, il faut multiplier chaque élément par son poids correspondant, puis additionner tous les produits obtenus et diviser le résultat par la somme des poids. Mathématiquement, cela peut être représenté de la manière suivante :
Moyenne pondérée = (élément 1 poids 1 + élément 2 poids 2 + … + élément n * poids n) / (poids 1 + poids 2 + … + poids n)
Utilisation d’une calculatrice pour calculer la moyenne pondérée
La plupart des calculatrices scientifiques ont une fonction intégrée pour calculer la moyenne pondérée. Voici les étapes générales pour utiliser une calculatrice pour effectuer ce calcul :
- Entrer les éléments de données et leurs poids correspondants dans une liste ou un tableau.
- Utiliser la fonction de la calculatrice pour multiplier chaque élément par son poids.
- Additionner tous les produits obtenus.
- Utiliser la fonction de la calculatrice pour additionner les poids.
- Diviser la somme des produits par la somme des poids pour obtenir la moyenne pondérée.
Il est important de se familiariser avec les fonctions de votre calculatrice spécifique pour effectuer ces étapes. Référez-vous au manuel d’utilisation de votre calculatrice si nécessaire.
Pertinence de la moyenne pondérée dans différents contextes
La moyenne pondérée est largement utilisée dans de nombreux domaines pour tenir compte de l’importance relative des éléments d’un ensemble de données. Voici quelques exemples de son utilisation dans différents contextes :
- Évaluation scolaire : Les professeurs utilisent souvent la moyenne pondérée pour calculer les notes finales des étudiants en attribuant des poids plus élevés aux examens ou aux travaux plus importants.
- Finance : Dans le domaine financier, la moyenne pondérée est utilisée pour calculer les indices boursiers en donnant plus de poids aux actions des grandes entreprises.
- Échantillonnage : Lors de la collecte d’échantillons statistiques, la moyenne pondérée permet de donner plus de poids à certains échantillons représentatifs d’une population donnée.
- Évaluation des performances : Dans le milieu professionnel, la moyenne pondérée est utilisée pour évaluer les performances des employés en attribuant des poids différents à différentes catégories d’évaluation.
Ces exemples soulignent l’importance de la moyenne pondérée dans de nombreux domaines et démontrent son utilité pour tenir compte de la variabilité et de la pertinence des données.
Choix des poids appropriés
Le choix des poids dans le calcul de la moyenne pondérée dépend du contexte et des objectifs de l’analyse. Il n’y a pas de règle stricte pour déterminer les poids appropriés, mais voici quelques considérations à prendre en compte :
- Importance relative : Les éléments les plus importants devraient avoir des poids plus élevés. Par exemple, dans une évaluation scolaire, un examen final pourrait avoir un poids plus élevé qu’un quiz hebdomadaire.
- Fiabilité des données : Les données de meilleure qualité ou plus fiables devraient avoir des poids plus élevés. Par exemple, lors d’une enquête, les réponses de personnes experts dans le domaine peuvent être pondérées plus lourdement que celles de participants moins informés.
- Objectifs de l’analyse : Les poids peuvent être choisis en fonction des objectifs spécifiques de l’analyse. Par exemple, dans une étude sur l’obésité infantile, l’indice de masse corporelle peut être pondéré plus lourdement que d’autres facteurs de risque.
Il est important de noter que les poids choisis doivent être justifiés et transparents pour garantir une analyse valide et crédible.
Exemples illustrant l’utilisation de la moyenne pondérée
Pour mieux comprendre comment la moyenne pondérée est utilisée dans la pratique, examinons quelques exemples concrets :
- Exemple 1 : Calcul de la moyenne pondérée des notes scolaires
- Note de l’examen final : 80 (poids = 40%)
- Note du travail de groupe : 90 (poids = 30%)
- Note du devoir à domicile : 70 (poids = 30%)
Moyenne pondérée = (80 0,4 + 90 0,3 + 70 * 0,3) / (0,4 + 0,3 + 0,3) = 80,33
La moyenne pondérée des notes est donc de 80,33.
- Exemple 2 : Calcul de l’indice boursier
- Valeur de l’action A : 1000 (poids = 50%)
- Valeur de l’action B : 2000 (poids = 30%)
- Valeur de l’action C : 1500 (poids = 20%)
Moyenne pondérée = (1000 0,5 + 2000 0,3 + 1500 * 0,2) / (0,5 + 0,3 + 0,2) = 1500
L’indice boursier est donc de 1500.
Ces exemples illustrent comment la moyenne pondérée peut être utilisée pour obtenir une mesure plus précise en tenant compte de l’importance relative des éléments.
Calcul plus détaillé :
Pour calculer la moyenne pondérée, vous devez multiplier chaque valeur par son poids, puis additionner tous les produits et diviser le résultat par la somme des poids. La formule mathématique est la suivante :
Moyenne pondérée = (valeur1 * poids1 + valeur2 * poids2 + … + valeurn * poidsn) / (poids1 + poids2 + … + poidsn)
Par exemple, si vous avez les valeurs 3, 5 et 7 avec des poids respectifs de 2, 3 et 1, la moyenne pondérée serait :
(3*2 + 5*3 + 7*1) / (2 + 3 + 1) = (6 + 15 + 7) / 6 = 28 / 6 = 4.67
Signification et applications :
La moyenne pondérée est largement utilisée dans de nombreux domaines tels que la finance, l\’éducation, la statistique, la gestion de projet, etc. En finance, elle est utilisée pour calculer les rendements pondérés des actifs financiers. En éducation, elle est utilisée pour calculer les notes finales des étudiants en tenant compte du poids de chaque évaluation. En gestion de projet, elle est utilisée pour calculer le coût moyen pondéré des ressources utilisées.
En conclusion, la moyenne pondérée est une méthode puissante pour calculer une moyenne plus précise en tenant compte du poids de chaque valeur. Sa polyvalence et ses nombreuses applications en font un outil essentiel dans de nombreux domaines.
Concept de Variation en Pourcentage
La variation en pourcentage est un concept mathématique important qui mesure le changement relatif d\’une valeur par rapport à une valeur de base. Elle est couramment utilisée dans de nombreux domaines pour analyser les tendances et les performances. La moyenne pondérée en pourcentage est une méthode spécifique pour calculer la variation en pourcentage en tenant compte des poids attribués à chaque valeur.
Applications
La moyenne pondérée en pourcentage est largement utilisée dans le domaine financier pour calculer le rendement des investissements. Par exemple, un investisseur pourrait utiliser la moyenne pondérée en pourcentage pour évaluer le rendement global de son portefeuille en tenant compte des poids attribués à chaque actif.
Dans le domaine de la gestion d\’entreprise, la moyenne pondérée en pourcentage est utilisée pour calculer les variations des ventes, des coûts et des profits. Cela permet aux gestionnaires de prendre des décisions éclairées basées sur les performances passées.
En conclusion, la moyenne pondérée est un outil mathématique essentiel pour calculer une moyenne en attribuant des poids différents à chaque élément. Son utilisation est pertinente dans de nombreux contextes et permet de tenir compte de l’importance relative des données. L’utilisation d’une calculatrice facilite grandement les calculs, mais il est important de comprendre les principes sous-jacents et de choisir des poids appropriés en fonction de la situation donnée. En utilisant la moyenne pondérée de manière judicieuse, il est possible de réaliser des analyses plus précises et basées sur des données solides.
Éléments interactifs
- Exercices interactifs : Proposez des exercices pratiques où les apprenants peuvent calculer la moyenne pondérée en pourcentage pour différentes situations. Par exemple, demandez-leur de calculer le rendement moyen d\’un portefeuille d\’actions en utilisant la méthode de la moyenne pondérée en pourcentage.
- Études de cas du monde réel : Présentez des études de cas du monde réel où la moyenne pondérée en pourcentage a été utilisée avec succès pour analyser les performances. Par exemple, montrez comment une entreprise a utilisé la moyenne pondérée en pourcentage pour évaluer l\’efficacité de ses campagnes marketing.
- Outils de visualisation : Fournissez des outils de visualisation tels que des graphiques et des tableaux pour aider les apprenants à comprendre visuellement le concept de variation en pourcentage. Par exemple, créez un graphique en camembert montrant la répartition des poids pour différents actifs dans un portefeuille d\’investissement.
| Méthode de mesure | Principe de mesure | Précision | Facilité d\’utilisation | Coût | Applications typiques | Exemples |
|---|---|---|---|---|---|---|
| Méthode A | Principe A de mesure | Haute | Facile | Élevé | Application A1, Application A2 | Exemple A1, Exemple A2 |
| Méthode B | Principe B de mesure | Moyenne | Modérée | Moyen | Application B1, Application B2 | Exemple B1, Exemple B2 |
| Méthode C | Principe C de mesure | Basse | Difficile | Bas | Application C1, Application C2 | Exemple C1, Exemple C2 |